坐标变换—PARK变换&CLARK变换(转载)

在对交流电动机数学模型进行化简得过程中，需要引进不同的坐标系，并将某些物理量在不同坐标系之间进行变换，这就叫坐标比那换。常用的坐标系如下图所示，（a）为ABC三坐标轴构成的三相静止坐标系，即三相ABC定子坐标系（3s坐标系），每个坐标轴上有一个等效绕组；（b）为静止的两相平面直角坐标系（2s坐标系），其中 α 轴与A轴重合， β 轴超前 α 轴90°，同样两个坐标轴（ αβ ）上分别各有一个绕组；（c）为以速度 ω 旋转的平面直角坐标系（2r坐标系），两个坐标系（dq，其中q轴超前d轴90°）上分别各有一个绕组^[1]。

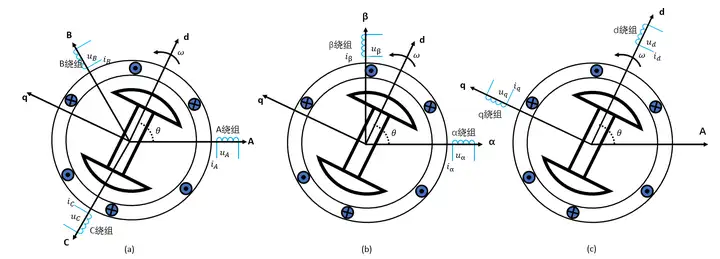
如果电动机的定子三相绕组可以采用dq坐标系，此时dq坐标系与转子坐标系重合。等效的定子绕组与转子坐标系相对静止，定子绕组与转子绕组之间的互感就不会与转子位置θ无关了，电感矩阵将会得到极大的简化。

电动机内的气隙磁场是进行电磁能量传递的媒介，定、转子间能量的传递正是通过气隙磁场进行的。不同类型绕组进行变换时，需要保证它们产生的总磁动势不变。只有遵守这一原则，才能保证电动机能量转换关系不变。

图（a）中三相对称定子绕组的每相匝数均为 N3 ，那么三相绕组产生的磁动势空间矢量在静止坐标系中采用复数可以表示为：

f3s2s=N3(iA+iBej2π3+iCej4π3)

公式中下标3s为该磁动势由3坐标系绕组产生，上标2s为描述该磁动势的坐标系，这里即是两相静止 αβ 坐标系。

图（b）中两相静止绕组的每相绕组匝数为 N2 ，两相绕组产生的磁动势空间矢量为：

f2s2s=N2(iα+iβejπ2)

图（c）中两相旋转绕组的每相绕组匝数为 N2 ，两相绕组产生的磁动势空间矢量为：

f2s2r=N2(id+iqejπ2)⋅ejθ

1 变换矩阵推导

令ABC三相对称定子绕组与两相静止 αβ 绕组产生的磁动势相等： f3s2s=f2s2s

可以推导出： (iα+iβejπ2)=N3N2(iA+iBej2π3+iCej4π3)

通常取 N3N2=23 ，这样推导的三相电流与两相电流的幅值相等，当 N3N2=23 时，三相电流与两相电流的功率相等。以下公式我们以等幅变换的情况进行举例（ N3N2=23 ），可以推导出3s坐标系中ABC绕组电流与2s坐标系中 αβ 绕组电流的变换矩阵：

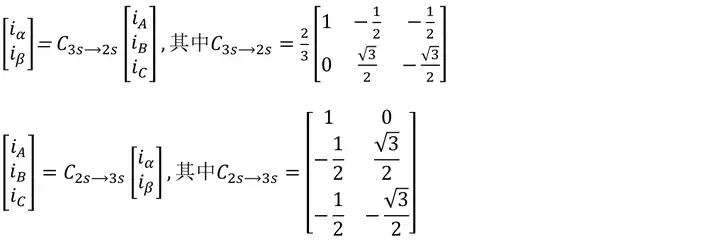
令两相静止 αβ 绕组与两相旋转dq绕组产生的磁动势相等： f322s=f2s2r

可以推导出： (iα+iβejπ2)=(id+iqejπ2)⋅ejθ

根据以上公式可以推导出2s坐标系中 αβ 绕组的电流与2r坐标系中dq绕组的电流之间的变换矩阵：

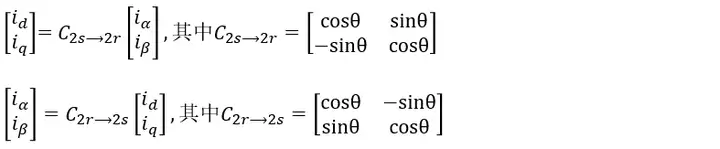
我们将各个坐标系之间的变换做了如下分类：

• clark 变换：将静止的ABC坐标系变换到静止的αβ坐标系（ C3s→2s ）
• clark逆变换：将静止的αβ坐标系变换到静止的ABC坐标系（ C2s→3s ）
• Park 变换：将静止的ABC坐标系变换到旋转的dq坐标系（ C3s→2r=C2s→2r⋅C3s→2s ）
• Park逆变换：将旋转的dq坐标系变换到静止的ABC坐标系（ C2r→3s=C2s→3s⋅C2r→2s ）

2 等幅变换系数推导

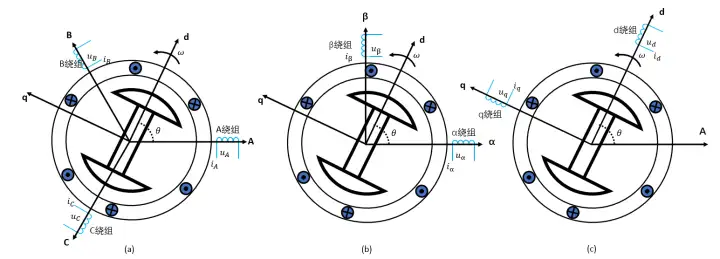
三相逆变输出的三相电压UA，UB，UC作用于电机，在三相平面静止坐标系ABC中，电压方程满足以下公式：

公式中 ω 为电位移角速度； Um 为相电压基波峰值。

由ABC轴矢量合成的电压矢量Vδ的表达式^[2]：

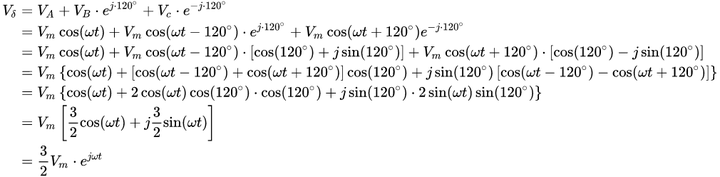
从上式可以看出，合成的电压矢量幅值是原幅值的32倍，因此为了等幅变换，所以 N3N2=23

3 等功率变换下的坐标变换

当 N3N2=23 时，三相电流与两相电流的功率相等，此时变换矩阵如下所示：

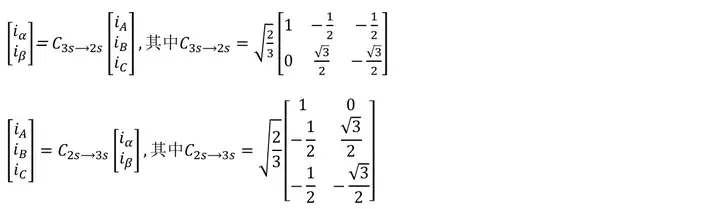
可以进行验算：C3s→2s⋅C2s→3s 是一个二维单位矩阵；C2s→3s⋅C3s→2s的结果虽然不是三位单位矩阵，但是对于三相三线系统中的一组变量（电压、电流、磁链等），若满足三相变量之和等于0，其坐标变换结果与三维单位矩阵是等效的。物理量在经过两次变换后均能够保持不变^[3]。

参考

1. ^《永磁同步电动机变频调速系统及其控制》
2. ^手撕系列（2）：Clark变换与Park变换 https://zhuanlan.zhihu.com/p/293470912
3. ^《永磁同步电动机变频调速系统及其控制》 P32

转载链接：https://zhuanlan.zhihu.com/p/507115686